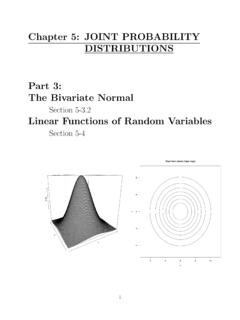
3 Random vectors and multivariate normal distribution

1 CHAPTER3ST 732,M. DAVIDIAN3 Randomvectorsandmultivariatenormaldistri butionAswe saw in Chapter1, a naturalway to thinkaboutrepeatedmeasurement datais as a seriesofrandomvectors, onevectorcorrespondingto each in which thesevectorsofmeasurements turnoutis governedby probability, we needtodiscussextensionsof usualunivari-ateprobability distributionsfor(scalar)randomvariablest omultivariateprobability ,it is wiseto reviewtheimportant conceptsof randomvariableandprobability distributionandhow we usetheseto :We may thinkof arandomvariableYas a characteristicwhosevaluesmayvary. Theway it takes onvaluesis described by aprobability ,REPEATED:It is customaryto useupper caseletters, , to denotea genericrandomvariableandlower caseletters, , to denotea particularvaluethattherandomvariablemay take onor thatmay be observed(data).

2 EXAMPLE:Supposewe areinterestedin thecharacteristic\bodyweight of rats"in thepopulationofallpossibleratsof a certainage,gender,andtype. We might letY=bodyweight of a (randomlychosen) a may conceptualizethatbodyweights of ratsaredistributedin thispopulationin thesensethatsomevaluesaremorecommon( them) we randomlyselecta ratfromthepopulation,thenthechanceit hasa certainbodyweight willbe governedby thisdistributionof weights in , valuesthatYmay take onaredistributedin thepopulationaccordingto anassociatedprobability distributionthatdescribes how likelythevaluesarein a moment, we willconsidermorecarefullywhyratweights we might seevary. First,we 32 CHAPTER3ST 732,M. DAVIDIAN(POPULATION)MEANANDVARIANCE:Reca llthatthemeanandvarianceof a probabilitydistributionsummarizenotionso f \center"and\spread"or \variability" of all randomvariableYwithanassociatedprobabili ty be thought of as theaverageof allpossiblevaluesthatYcouldtake on,so theaverageof (aremorelikely)thanothers,so thisaveragere writeE(Y):( )todenotethisaverage,thepopulationmean.

3 TheexpectationoperatorEdenotesthatthe\av eraging"operationover allpossiblevaluesof itsargument is to be , theaveragemay be thought of as a \weighted"average,whereeach possiblevalueis representedin accordancetotheprobabilitywithwhich it occursin \ " is be thought of as a way of describingthe\center"of thedistributionof alsoreferredto as we have arandomsampleof observationsona randomvariableY, sayY1; : : : ; Yn, thenthesamplemeanis justtheaverageof these:Y=n 1nXj=1Yj:For example,ifY= ratweight, andwe wereto obtaina randomsampleofn= 50 ratsandweigheach,thenYrepresents theaveragewe wouldobtain. Thesamplemeanis a naturalestimatorforthepopulationmeanof theprobability distributionfromwhich therandomsamplewas be thought of as measuringthespreadof allpossiblevaluesthatmaybe observed,basedonthesquareddeviationsof each valuefromthe\center"of thedistributionof , varianceis basedonaveragingsquareddeviationsacrosst hepopulation,which is representedusingtheexpectationoperator,a ndis givenbyvar(Y) =Ef(Y )2g; =E(Y):( )( )showstheinterpretationof varianceas anaverageof squareddeviationsfromthemeanacrossthepop ulation,takinginto account thatsomevaluesaremorelikely(occurwithhig herprobability) 33 CHAPTER3ST 732,M.

4 DAVIDIAN Theuseof squareddeviationstakes into account magnitudeof thedistancefromthe\center"butnotdirectio n,so is attemptingto measureonly\spread"(ineitherdirection).T hesymbol \ 2" is oftenusedgenericallyto represent showstwo normaldistributionswiththesamemeanbutdi erent variances 21< 22, illustratinghow variancedescribesthe\spread"of :Normaldistributionswithmean butdi erentvariances PSfragreplacements 21 22 Varianceis onthescaleof theresponse, measureof spreadthatis onthesamescaleas theresponseis thepopulationstandarddeviation, de nedaspvar(Y). Thesymbol is randomsampleas above, thesamplevarianceis (almost)theaverageof thesquareddeviationsof each observationYjfromthesamplemeanY :S2= (n 1) 1nXj=1(Yj Y)2: Thesamplevarianceis usedas (n 1) ratherthannis usedso thattheestimatorisunbiased, thesamplesizenis small.

5 Thesamplestandarddeviationis justthesquareroot of thesamplevariance,oftenrepresentedby 34 CHAPTER3ST 732,M. DAVIDIANGENERALFACTS:Ifbis a xedscalarandYis a randomvariable,then E(bY) =bE(Y) =b ; theaveragearejustmultipliedbyb. Also,E(Y+b) =E(Y) +b; addinga constant to each valuein thepopulationwilljustshifttheaverageby thissameamount. var(bY) =Ef(bY b )2g=b2var(Y); theaveragearejustmultipliedbyb2. Also,var(Y+b) = var(Y); addinga constant to each valuein thepopulationdoes nota ecthow theyvaryaboutthemean(which is alsoshiftedby thisamount).SOURCESOFVARIATION:We now considerwhy thevaluesof a characteristicthatwe might observevary. Consideragaintheratweight example. Biological is well-knownthatbiologicalentitiesaredi erent; althoughlivingthingsof thesametype tendto be similarin theircharacteristics,theyarenotexactlyth esame(exceptperhapsin thecaseof genetically-identicalclones).

6 Thus,evenif we focusonratsof thesamestrain,age,andgender,we expectvariationin thepossibleweights of such ratsthatwe mightobserve dueto inherent, theweight of a randomlychosenrat,withprobability distributionhavingmean . If allratswerebiologicallyidentical,thenthe populationvarianceofYwouldbe equalto 0,andwe wouldexpectallratsto have exactlyweight . Ofcourse,becauseratweights varyas aconsequenceof biologicalfactors,thevarianceis>0, andthus theweight of a randomlychosenratis notequalto butratherdeviatesfrom by somepositive or negative amount. Fromthisview,we might thinkofYas beingrepresentedbyY= +b;( )wherebis a randomvariable,withpopulationmeanE(b) = 0 andvariancevar(b) = 2b, ,Yis \decomposed"into itsmeanvalue(asystematiccomponent) andarandomdevia-tionbthatrepresents by how much a ratweight might deviatefromthemeanratweight duetoinherent biologicalfactors.

7 ( )is a simplestatisticalmodelthatemphasizesthat we believe ratweights we might seevarybecauseof ( )impliesthatE(Y) = andvar(Y) = 35 CHAPTER3ST 732,M. DAVIDIAN have discussedratweight as though,oncewe have a ratin hand,wemay know itsweight exactly. However,a scaleusuallymustbe , a scaleshouldregisterthetrueweight of an itemeach timeit is weighed,but,becausesuch devicesareimperfect,measurements on thesameitemmay by which themeasurementdi ersfromthetruthmay be thought of as anerror; deviationupor downfromthetruevaluethatcouldbe observedwitha \perfect" \fair"orunbiaseddevicedoes notsystematicallyregisterhighor low mostof thetime;rather,theerrorsmay go in ,if we onlyhave anunbiasedscaleonwhich to weighrats,a ratweight we might observere ectsnotonlythetrueweight of therat,which variesacrossrats,butalsotheerrorin takingthemeasurement.

8 We might thinkof a randomvariablee, say, thatrepresents theerrorthatmightcontaminatea measurement of ratweight, takingon possiblevaluesin a hypothetical\population"of allsuch errorsthescalemight stillbelieve ratweights varydueto biologicalvariation,butwhatwe seeis alsosubjecttomeasurement thus makes senseto reviseourthinkingof whatYrepresents,andthinkofY= \measuredweight of a randomlychosenrat."Thepopulationof allpossiblevaluesYcouldtake onis allpossiblevaluesof ratweight we might measure; ,allvaluesconsistingof atrueweight of a ratfromthepopulationof allratscontaminatedby a measurement errorfromthepopulationof allpossiblesuch ,it is naturalto representYasY= +b+e= + ;( )wherebis as in ( ).eis thedeviationdueto measurement error,withE(e) = 0 andvar(e) = 2e, ( ), =b+erepresents theaggregatedeviationduetothee ectsofbothbiologicalvariationandmeasurem ent ,E( ) = 0 andvar( ) = 2= 2b+ 2e, so thatE(Y) = andvar(Y) = 2accordingto themodel( ).

9 Here, 2re ectsthe\spread"of measuredratweights anddependsonboththespreadin trueratweightsandthespreadin errorsthatcouldbe committedin variationthatwe couldconsider;we deferdiscussionto laterin now,theimportant messageis that,in consideringstatisticalmodels,it is criticalto beawareof di erentsourcesof variationthatcauseobservationsto vary. Thisis especiallyimportantwithlongitudinaldata, as we 36 CHAPTER3ST 732,M. DAVIDIANWe now considertheseconceptsin thecontextof a each xedvaluex1; : : : ; xn, we observe a correspondingrandomvariableYj,j= 1; : : : ; n. For example,supposethatthexjaredosesof a eachxj, a ratis rat(givendosexj) may be usuallystatedisYj= 0+ 1xj+ j;where jis a randomvariablewithmean0 andvariance 2; thatisE( j) = 0;var( j) = 2:Thus,E(Yj) = 0+ 1xjandvar(Yj) = that,ideally, at eachxj, theresponseof interest,Yj, shouldbe exactlyequalto the xedvalue 0+ 1xj, themeanofYj.

10 However,becauseof factorslike (i)biologicalvariationand(ii)measurement error,thevalueswe might seeatxjvary. In themodel, jrepresents thedeviationfrom 0+ 1xjthatmight occurbecauseof theaggregatee ectof thesesourcesof a continuousrandomvariable,it is oftenthecasethatthenormaldistributionis a reasonableprobability modelforthepopulationof jvalues;thatis, j N(0; 2):Thissays thatthetotale ectof allsourcesof variationis to createdeviationsfromthemeanofYjthatmay be equallylikelyin eitherdirectionas dictatedby thesymmetricnormalprobability ,we have thatthepopulationof observationswe might seeat a particularxjisalsonormalandcenteredat 0+ 1xj; N( 0+ 1xj; 2): Thismodelsays thatthechanceof seeingYjvaluesabove or below themean 0+ 1xjis thesame(symmetry).