A SAMPLE RESEARCH PAPER/THESIS/DISSERTATION ON …

1 A SAMPLE RESEARCH PAPER/THESIS/DISSERTATION ON ASPECTS OFELEMENTARY LINEARY ALGEBRAbyJames , Southern Illinois University, 2010A RESEARCH paper / thesis /DissertationSubmitted in Partial Fulfillment of the Requirements for theMaster of Science DegreeDepartment of Mathematicsin the Graduate SchoolSouthern Illinois University CarbondaleJuly, 2006(Please replace Name and Year with your information and delete all instructions)Copyright by NAME, YEARAll Rights Reserved**(This page is optional)** RESEARCH PAPER/THESIS/DISSERTATION APPROVALTITLE (in all caps)By(Author)A thesis / dissertation Submitted in PartialFulfillment of the Requirementsfor the Degree of(Degree)in the field of (Major)Approved by:(Name of thesis / dissertation chair), Chair(Name of committee member 1)(Name of committee member 2)(Name of committee member 3)(Name of committee member 4)Graduate SchoolSouthern Illinois University Carbondale(Date of Approval)AN ABSTRACT OF THE dissertation OFNAME OF STUDENT, for the Doctor of Philosophy degree in MAJORFIELD, presented on DATE OF DEFENSE, at Southern Illinois University Car-bondale.

2 (Do not use abbreviations.)TITLE: A SAMPLE RESEARCH paper ON ASPECTS OF ELEMENTARYLINEAR ALGEBRAMAJOR PROFESSOR: Dr. J. Jones(Begin the abstract here, typewritten and double-spaced. Athesis abstractshould consist of 350 words or less including the heading. A page and one-half isapproximately 350 words.)iiiDEDICATION(NO REQUIRED FOR RESEARCH paper )(The dedication, as the name suggests is a personal dedication of one s section is OPTIONAL and should be double-spaced if included in the the-sis/ dissertation .)ivACKNOWLEDGMENTS( NOT REQUIRED IN RESEARCH paper )I would like to thank Dr. Jones for his invaluable assistanceand insights leadingto the writing of this paper . My sincere thanks also goes to the seventeen membersof my graduate committee for their patience and understanding during the nineyears of effort that went into the production of this special thanks also to Howard Anton [1], from whose book many of theexamples used in this SAMPLE RESEARCH paper have been quoted.

3 Another specialthanks to Prof. Ronald Grimmer who provided the previous thesis template uponwhich much of this is based and for help with graphics (DO NOT USE IN RESEARCH paper )A preface or foreword may contain the author s statement of the purpose ofthe study or special notes to the reader. This section is OPTIONAL and should bedouble-spaced if used in the OF CONTENTSA bstract .. iiiDedication .. ivAcknowledgments ..vPreface .. viList of Tables .. viiiList of Figures .. ixIntroduction ..11 Systems of Linear Equations and Matrices .. Introductions to Systems of Linear Equations .. Gaussian Elimination .. Further Results on Systems of Equations .. Some Important Theorems ..62 Determinants .. The Determinant Function .. Evaluating Determinants by Row Reduction.

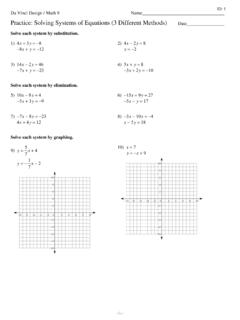
4 Some Final Conclusions .. Properties of the Determinant Function ..83 Examples .. 11 References .. 16 Appendix .. 16 Vita .. 19viiLIST OF An example table showing how centering works with extended captioning. 9viiiLIST OF (a) no solution, (b) one solution, (c) infinitely many solutions .. Inside and outside numbers of a matrix multiplication problem ofA B=AB, showing how the inside dimensions are dropped and the dimensionsof the product are the outside dimenions.. An encapsulated postscript file.. A second encapsulated postscript file.. Two rows of graphics: (a) Square (b) Circle (c) Rectangle.. Three rows of graphics: (a) (c) Squares. (d) (f) Circles. (g) (i) Ovals. Use of verbatim environment .. Matrix Rotated 90 degrees.

5 15ixINTRODUCTIONThis paper provides an elementary treatment of linear algebra that is suitablefor students in their freshman or sophomore year. Calculus is not a aim in writing this paper is to present the fundamentals of linear alge-bra in the clearest possible way. Pedagogy is the main consideration. Formalismis secondary. Where possible, basic ideas are studied by means of computationalexamples and geometrical treatment of proofs varies. Those proofs that are elementary and hve sig-nificant pedagogical content are presented precisely, in a style tailored for few proofs that are more difficult, but pedgogically valuable, are placed at the endof of the section and marked Optional . Still other proofs are omitted completely,with emphasis placed on applying the 1 deals with systems of linear equations, how to solve them, andsome of their properties.

6 It also contains the basic material on matrices and theirarithmetic 2 deals with determinants. I have used the classicalpermutationapproach. This is less abstract than the approach throughn-linear alternative formsand gives the student a better intuitive grasp of the subjectthan does aninductive 3 introduces vectors in 2-space and 3-space as arrows and develops theanalytic geometry of lines and planes in 3-space. Dependingon the background ofthe students, this chapter can be omitted without a loss of 1 SYSTEMS OF LINEAR EQUATIONS AND INTRODUCTIONS TO SYSTEMS OF LINEAR EQUATIONSIn this section we introduce base terminology and discuss a method for solvingsystems of linear line in thexy-plain can be represented algebraically by an equation of theforma1x+a2y=bAn equation of this kind is called a linear equation in the variablesxandy.

7 Moregenerally, we define a linear equation in thenvariablesx1, .. , xnto be one thatcan be expressed in the forma1x1+a2x2+ +anxn=b( )wherea1, a2, .. anandbare real finite set of linear equations in the variablesx1, x2, .. , xnis calledasystem of linear all systems of linear equations has solutions. A system of equations thathas no solution is said to beinconsistent. If there is at least one solution, it iscalledconsistent. To illustrate the possibilities that can occur in solving systems oflinear equations, consider a general system of two linear equations in the unknownsxandy:a1x+b1y=c1a2x+b2y=c22 The graphs of these equations are lines; call theml1andl2. Since a point (x, y) lieson a line if and only if the numbersxandysatisfy the equation of the line, thesolutions of the system of equations will correspond to points of intersection ofl1andl2.

8 There are three possibilities:DDDDDDDDDDDDDDDDl1l2(a) DDDDDDDDl1l2(b) l1, l2(c)Figure (a) no solution, (b) one solution, (c) infinitelymany solutionsThe three possiblities illustrated in Figure are as follows:(a)l1andl2are parallel, in which case there is no intersection, and consequentlyno solution to the system.(b)l1andl2intersect at only one point, in which case the system has exactly (c)l1andl2coincide, in which case there are infinitely many points of intersection,and consequently infinitely many solutions to the we have considered only two equations with two unknowns here, wewill show later that this same result holds for arbitrary systems; that is, every systemof linear equations has either no solutions, exactly one solution, or infinitely GAUSSIAN ELIMINATIONIn this section we give a systematic procedure for solving systems of linearequations.

9 It is based on the idea of reducing the augmented matrix to a form thatis simple enough so that the system of equations can be solvedby is not difficult to see that a matrix in row-echelon form musthave zerosbelow each leading 1. In contrast a matrix in reduced row-echelon form must havezeros above and below each leading a direct result of Figure on page 3 we have the homogenous system of linear equations with more unknownsthan equations always has infinitely many solutionsThe definition of matrix multiplication requires that the number of columns ofthe first factorAbe the same as the number of rows of the second factorBin orderto form the productAB. If this condition is not satisfied, the product is convenient way to determine whether a product of two matrices is defined is towrite down the size of the first factor and, to the right of it, write down the size ofthe second factor.

10 If, as in Figure , the inside numbers are the same, then theproduct is defined. The outside numbers then give the size of the rAr nB=m nABoutsideinsideFigure Inside and outside numbers of a matrix multiplica-tion problem ofA B=AB, showing how the inside dimensionsare dropped and the dimensions of the product are the the commutative law for multiplication is not valid in matrix arith-metic, many familiar laws of arithmetic are valid for matrices. Some of the mostimportant ones and their names are summarized in the following that the sizes of the matrices are such that the in-dicated operations can be performed, the following rules ofmatrix arithmetic arevalid.(a)A+B=B+A(Commutative law for addition)(b)A+ (B+C) = (A+B) +C(Associative law for addition)(c)A(BC) = (AB)C(Associative law for multiplication) FURTHER RESULTS ON SYSTEMS OF EQUATIONSIn this section we shall establish more results about systems of linear equationsand invertibility of matrices.