CONVERT QUADRATIC FUNCTIONS FROM ONE FORM TO …

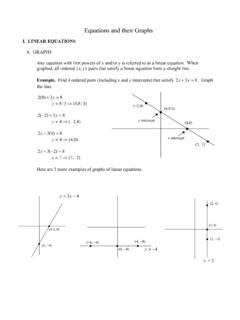
1 CONVERT QUADRATIC FUNCTIONS FROM ONE FORM TO ANOTHER (Standard Form <==> Intercept Form <==> Vertex Form) (By Nghi H Nguyen Dec 08, 2014) 1. THE QUADRATIC FUNCTION IN INTERCEPT FORM The graph of the QUADRATIC function in standard form, f(x) = ax + bx + c, is a parabola that may intercept the x-axis at 2 points, unique point, or no point at all. This means a QUADRATIC equation f(x) = ax + bx + c = 0 may have 2 real roots, one double real root, or no real roots at all (complex roots). We can write f(x) in the form: y = a(x + bx/a + c/a) (1). Recall the development of the QUADRATIC formula: x + bx/a + (b /4a - b /4a ) + c/a = 0 (x + b/2a) - (b - 4ac)/4a = 0 (x + b/2a) - d /4a = 0.

2 (Call d = b - 4ac) (x + b/2a + d/2a)(x + b/2a d/2a) = 0 (2) Replace this expression (2) into the equation (1), we get the QUADRATIC function f(x) written in intercept form: f(x) = a(x x1)(x x2) (x1 and x2 are the 2 x-intercepts, or roots of f(x) = 0) f(x) = a(x + b/2a + d/2a)(x + b/2a d/2a) (3) 2. THE QUADRATIC FORMULA IN INTERCEPT FORM From the equation (3), we deduct the formula: x = -b/2a d/2a (4) In this formula, x being the 2 roots of the QUADRATIC equation f(x) = 0: - The quantity ( b/2a) represents the x-coordinate of the parabola axis. - The 2 quantities (d/2a) and (-d/2a) represent the 2 distances AB and AC from the parabola axis to the two x-intercepts (real roots) of the parabola.

3 - The quantity d can be zero, a number (real or radical), or imaginary number. - If d = 0: there is a double root at x = -b/2a. - If d is a number (real or radical), there are two x-intercepts, meaning two real roots. - If d is imaginary, there are no real roots. The parabola doesn t intercept the x-axis. - The unknown quantity d can be computed from the constants a, b, c by this relation (5): d = b 4ac (5) We can easily obtain this relation by writing that the product (x1*x2) of the 2 real roots is equal to (c/a). (-b/2a + d/2a)(-b/2a d/2a) = c/a b d = 4ac d = b 4ac If d = 0, there is double root at x = -b/2a If d > 0, there are 2 real roots.

4 If d < 0, there are no real roots, there are complex roots. Page 2 of 9 To solve a QUADRATIC equation, first find the quantity d by the relation (5), then find the 2 real roots by the formula (4). REMARK. This new QUADRATIC formula in intercept (graphic) form is simpler and easier to remember than the classic formula since students can relate it to the x-intercepts of the parabola graph. In addition, the two quantities (d/2a) and (-d/2a) make more sense about distance than the classical quantity: (b^2 4ac). 3. CONVERT QUADRATIC EQUATIONS FROM STANDARD FORM TO VERTEX FORM Problem.

5 Given f(x) = ax + bx + c. Find x1 and x2 to CONVERT f(x) to intercept form: f(x) = a*(x x1)(x x2) Solution. To CONVERT a function, from standard form f(x) = ax + bx + c, to intercept form, we use the general intercept form expression (3). f(x) = a*(x + b/2a + d/2a)(x + b/2a d/2a), with d = b - 4ac. a. If d is real, whole number ( 3, 14, ), or fraction ( 3/5, 23 ), there are 2 x-intercepts. f(x) can be factored and f(x) can be converted to intercept form. Examples: f(x) = (x 7)(x + 8); y = (x + 3)(x + 23); f(x)= (3x 5)(7x 13); y = (5x 7)(6x 5) b. If d is radical ( 5, 13, ), there are 2 x-intercepts.

6 F(x) can t be factored. However f(x) can be converted to intercept form. See Example 10 and 11. Examples: f(x) = (x 1/2 + 5/2)(x 1/2 - 5/2); f(x) = (x - 2/3 - 3/3)(x 2/3 + 3/3) c. If d is imaginary ( 3i, ), there are no x-intercepts, and there is no intercept form. Example 1. CONVERT y = 5x + 6x 8 into intercept form Solution. First find d = 36 + 160 = 196 d = 14 and d = - 14. Substitute the values of d, a, b, c into (3), we get y in intercept form. y = 5*(x + 6/10 + 14/10)(x + 6/10 14/10) y = 5*(x 4/5)(x + 2) = (5x 4)(x + 2). Page 3 of 9 Example 2. CONVERT y = 7x^2 + 18x 25 to intercept form Solution.

7 First find d = 324 + 700 = 1024 d = 32 and d = -32. y = 7*(x + 18/14 - 32/14)(x + 18/14 + 32/14) Intercept form: y = 7*(x - 1)(x + 25/7) = (x 1)(7x + 25) Example 3. CONVERT y = 16x + 34x 15 to intercept form. Solution. First find d = b 4ac = 1156 + 960 = 2116 d = 46 and d = -46 Since d is a whole number, we can either factor the equation, or use the formula. Factoring gives the intercept form: y = (8x 3)(2x + 5) Example 4. CONVERT y = 9x + 4x 1 to intercept form Solution. d = 16 + 36 = 52 = 4*13 d = 2 13 and d = -2 13. Replace values of d, a, b, c into the general expression (3).

8 Intercept form: y = 9[x + (2 + 13)/9)(x + (2 - 13)/9). y = 1/9(9x + 2 + 13)(9x + 2 - 13) Back check. We may check the answer by multiplying the 2 factors: y = 1/9[(9x + 2) - 13] = 1/9*(81x + 36x + 4 13) = 9x + 4x - 1 Example 5. CONVERT y = 9x - 12x + 1 to intercept form. Solution. d = 144 36 = 108 = 36*3 d = 6 3 and d = -6 3. Intercept form: y = 9(x - 2/3 + 3/3)(x - 2/3 - 3/3) = (3x 2 + 3)(3x 2 - 3) Back check. We may check the answer by multiplying the 2 factors: y = (3x 2) - 3 = 9x - 12x + 4 3 = 9x - 12x + 1 4. CONVERT QUADRATIC FUNCTIONS FROM STANDARD FORM TO VERTEX FORM We can CONVERT a QUADRATIC function from standard form, y = ax + bx + c, to the general vertex form: y = a(x + p) + q.]

9 We don t need to factor the QUADRATIC equation because factoring is only a special case of finding the 2 real roots. The below method is generally better. Problem. Given a QUADRATIC function in standard form: f(x) = ax + bx + c Find p and q to CONVERT f(x) to the Vertex Form: f(x) = a*(x + p) + q Recall the formula (4) of the QUADRATIC formula in intercept form: x = -b/2a d/2a. (4) Page 4 of 9 Solution. The quantity (-b/2a) represents the x-coordinate of the vertex. At the vertex, d = 0 since the horizontal distances of the vertex to the 2 related x-intercepts are zero. The y-coordinate of the vertex is f(-b/2a).

10 Consequently, the general vertex form of a QUADRATIC function can be written as: f(x) = a(x + b/2a) + f(-b/2a) (6) Example 1. CONVERT y = 5x + 6x 8 to vertex form. Solution. We have: a = 5; and (-b/2a) = -6/10 = -3/5; f(-3/5) = ax + bx + c = 5(9/25) 6(3/5) 8 = -49/5 The vertex form y = 5(x + 3/5) - 49/5 Example 2. CONVERT y = 7x + 18x 25 to vertex form. Solution. We have: a = 7; and (-b/2a) = -18/14 = -9/7 f(-9/7) = 7(81/49) 18(9/7) 25 = 81/7 162/7 175/7 = 256/7 The vertex form y = 7(x + 9/7) - 256/7. Example 3. CONVERT y = 2x + 9x + 10, to vertex form.