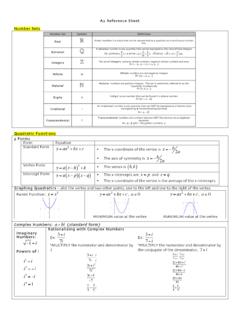
QUADRATIC EQUATIONS - El Paso Community …

1 QUADRATIC EQUATIONS A QUADRATIC equation is always written in the form of: axbxc20+ + = where a 0 The form axbxc20+ + = is called the standard form of a QUADRATIC equation. Examples: xx2560 + = This is a QUADRATIC equation written in standard form. 442 =+xx This is a QUADRATIC equation that is not written in standard form but can be once we set the equation to: xx2440+ + =. xx2= This too can be a QUADRATIC equation once it is set to 0. xx20 = (standard form with c=0). Solving QUADRATIC EQUATIONS by Square Root Property Whenax=2, where a is a real number, then your ax = Examples: 092= x 23 28y+= 092= x 23 3 28 3y+ = 92=x 225y= 9 =x 25y= 3 =x 5y= Solving QUADRATIC EQUATIONS by Factoring It can also be solved by factoring the equation.

2 Remember to always check your solutions. You can use direct substitution of the solutions in the equation to see if the solutions satisfy the equation. Examples: xx2560 + = ()()023= xx Factoring x xx ==303 xx ==202 Set it equal to 0 and solve for x Now check if, x = 3 and x = 2 are the solutions of xx2560 + = Check: 35 360915602 + = + =( ) 25 260410602 + = + =( ) 27402xx+ = ()()2140xx + = 2102112xxx === xx+ == 404 Another method of checking the solutions is by using one of the following statements: The sum of the solutions = ab or The product of the solutions = ca where a, b, and c are the coefficients in axbxc20+ + =.

3 Now we check if x = 21 and x = 4 are the solutions of 27402xx+ = Check: Using the sum of the solutions = 12472+ = () Based on the original equation = = ba72 Now by using the product of the solutions = 1242() = Based on the original equation = ca= = 422 22810xx+ = Rewrite in standard form by multiplying each side of the equation by x2 xx2280+ = ()()xx+ =420 x + 4 = 0 20x = 4x= x = 2 Check: ( )2281044+ = S olutions must be checked in the original equation to avoid any errors.

4 111022 = 2281022+ = 1 + 1 2 = 0 Solution Using the QUADRATIC Formula Factoring is useful only for those QUADRATIC EQUATIONS which have whole numbers. When you encounter QUADRATIC EQUATIONS that can not be easily factored out, use the QUADRATIC formula to find the value of x: xbbaca= 242 Examples: xx282 = xx2280+ = Rewrite in standard form, where 1 2 and 8a,b,c= == x= 244 182 1( )()( ) Plug in numbers into the equation = = 2362 1262( ) 24,= The two rational solutions 313402xx + = x= ()()( )()( )13134 342 32 61113612113 = = 62,624= =413, The two rational solutions In some cases you encounter repeated rational solutions.

5 And to prove you have the right values you use the discriminant which gives you information about the nature of the solutions to the equation. Based on the expression bac24 , which is under the radical in the QUADRATIC formula it can be found in the equation axbxc20+ + =. I. When the discriminant is equal to 0, the equation has repeated rational solutions. Example: xx2210 + = By using the discriminant bac22424 110 = =()( )( ) x= ()()( )( )( )224 112 12 = 202 11x,= Repeated rational solutions II. When the discriminant is positive and a perfect square, the equation has two distinct rational solutions. Example: xx2430 + = By discriminant bac22444 134 = =()( )( ) x= ()()( )( )( )444 132 12 = 442 31x,= Two distinct rational solutions III.

6 When the discriminant is positive but not a perfect square, the equation has two irrational solutions. Example: 0642= +xx The discriminant bac22444 1640 = =( )( )() x= 444 162 12( )( )()( ) = 4402 210x= Two irrational solutions IV. When the discriminant is negative, the equation has two complex number solutions. Example: xx2460+ + = The discriminant bac22444 168 = = ( )( )( ) x= 444 162 12( )( )( )( ) 482x = Two complex number solutions Solution by Completing the Square One more method of solving QUADRATIC EQUATIONS is by completing the square. Example: Solve 26 50xx+ += by completing the square.

7 1) If the leading coefficient is not 1, use the multiplication (or division) property of equality to make it 1: 26 50xx+ += In this case the leading coefficient is already 1 2) Rewrite the equation by sending the constant to the right side of the equation: 2226 506 55 0565xxxxxx+ +=+ + = += 3) Divide the numerical coefficient the middle term by 2, then square it, and add it to both sides of the equation, but leave the square form on the left side of the equation: ( )( )( )( )22222222656 3536 359634xxxxxxxx+= + + = ++ + = +++ = Middle term coefficient = 6 ( )26332= 4) Once you found the squared number rewrite the equation as follows: ( )22634xx++ = Bring down the variable x and put it inside the parentheses Use the sign of the middle term.

8 In this case it is +. ()234x+= Write the squared number. In this case it is 3. The resultant binomial is ()234x+= 5) Using the square root property clear the term. ()234x+= The square root of a squared term is the term by itself. 32x+= 6) Solve for the variable x. 32x+= The notation is used because the square root can have both positive and negative answers. 32x+= 32x+= () ( )221324 + = = And () ( )22532 4 + = = 23x= 23x= 1x= 5x= 7) Check your solution. ( )( )2216 501 6 1 5016 5 000xxx= + += + += +== Both solutions are true: ( )( )2256 505 6 5 5025 30 5 000xxx= + += + += +== Let s keep practicing with one more.

9 Example: 24 2 50xx = One way to make the leading coefficient 1 is ()( )2114 25044xx = by multiplying both sides of the equation by 14 215024xx = Move the constant to the right side of the equation 21524xx = 2221 1 512 4 44xx + =+ Divide the middle term coefficient by 2, square it, and add it to both sides of the equation: 21 2 11 11 21 22 44 = = 221 1 51244 16xx + =+ 2211212416xx + = 2121416x = Write the squared number in binomial form. 2121416x = Find the square root of both sides and don t forget the sign. 121416x = Send the other number to the right side of the equation.

10 12144x = Try to solve it using the square root. If not possible leave it in radical form. 21144x= + Solve for x. 1214x = Final answer. QUADRATIC EQUATIONS EXERCISES Solve each of the following EQUATIONS by the method of your choice and check your solutions. 1. xx2210 + = 2. xx29200+ + = 3. 351202xx = 4. 69602xx+ = 5. xx23280+ = 6. 32272xxx = + 7. 412162xx = 8. xx230+ = 9. 31102+ =xx 10. 3402yy = 11. yy2210+ + = 12. xx2280 = 13. x240+ = 14. xx21+ = 15. 96802yy+ = 16. y2250 = 17. 613602yy + = 18. xx = 4313 19.