Transcription of THE GAUSSIAN INTEGRAL - University of Connecticut
1 THE GAUSSIAN INTEGRALKEITH CONRADLetI= e 12x2dx, J= 0e x2dx,andK= e numbers are positive, andJ=I/(2 2) andK=I/ 2 . notation as above,I= 2 , or equivalentlyJ= /2, or equivalentlyK= will give multiple proofs of this result. (Other lists of proofs are in [4] and [9].) The theoremis subtle because there is no simple antiderivative fore 12x2(ore x2ore x2). For comparison, 0xe 12x2dxcan be computed using the antiderivative e 12x2: this INTEGRAL is proof : Polar coordinatesThe most widely known proof , due to Poisson [9, p. 3], expressesJ2as a double INTEGRAL andthen uses polar coordinates. To start, writeJ2as an iterated INTEGRAL using single-variable calculus:J2=J 0e y2dy= 0Je y2dy= 0( 0e x2dx)e y2dy= 0 0e (x2+y2) this as a double INTEGRAL over the first quadrant.
2 To compute it with polar coordinates, thefirst quadrant is{(r, ) :r 0 and 0 /2}. Writingx2+y2asr2and dxdyasrdrd ,J2= /20 0e r2rdrd = 0re r2dr /20d = 12e r2 0 2=12 2= >0,J= /2. It is argued in [1] that this method can t be applied to any other proof : Another change of variablesOur next proof uses another change of variables to computeJ2. As before,J2= 0( 0e (x2+y2)dx) CONRADI nstead of using polar coordinates, setx=ytin the inner INTEGRAL (yis fixed). Then dx=ydtand( )J2= 0( 0e y2(t2+1)ydt)dy= 0( 0ye y2(t2+1)dy)dt,where the interchange of integrals is justified by Fubini s theorem for improper Riemann integrals.
3 (The appendix gives an approach using Fubini s theorem for Riemann integrals on rectangles.)Since 0ye ay2dy=12afora >0, we haveJ2= 0dt2(t2+ 1)=12 2= 4,soJ= /2. This proof is due to Laplace [7, pp. 94 96] and historically precedes the widely usedtechnique of the previous proof . We will see in Section 9 what Laplace s first proof proof : Differentiating under the INTEGRAL signFort >0, setA(t) =( t0e x2dx) INTEGRAL we want to calculate isA( ) =J2and then take a square (t) with respect totand using the Fundamental Theorem of Calculus,A (t) = 2 t0e x2dx e t2= 2e t2 t0e , soA (t) = 2e t2 10te t2y2dy= 102te (1+y2) function under the INTEGRAL sign is easily antidifferentiatedwith respect tot:A (t) = 10 te (1+y2)t21 +y2dy= ddt 10e (1+y2)t21 + (t) = 10e t2(1+x2)1 +x2dx,we haveA (t) = B (t) for allt >0, so there is a constantCsuch that( )A(t) = B(t) +Cfor allt >0.
4 To findC, we lett 0+in ( ). The left side tends to( 00e x2dx)2= 0 whilethe right side tends to 10dx/(1 +x2) +C= /4 +C. ThusC= /4, so ( ) becomes( t0e x2dx)2= 4 10e t2(1+x2)1 + in this equation, we obtainJ2= /4, soJ= comparison of this proof with the first proof is in [20].THE GAUSSIAN proof : Another differentiation under the INTEGRAL signHere is a second approach to findingJby differentiation under the INTEGRAL sign. I heard aboutit from Michael Rozman [14], who modified an idea [22], and in a slightlyless elegant form it appeared much earlier in [18].Fort R, setF(t) = 0e t2(1+x2)1 + (0) = 0dx/(1 +x2) = /2 andF( ) = 0. Differentiating under the INTEGRAL sign,F (t) = 0 2te t2(1+x2)dx= 2te t2 0e (tx) the substitutiony=tx, with dy=tdx, soF (t) = 2e t2 0e y2dy= 2Je >0, integrate both sides from 0 toband use the Fundamental Theorem of Calculus: b0F (t) dt= 2J b0e t2dt= F(b) F(0) = 2J b0e in the last equation,0 2= 2J2= J2= 4= J= proof : A volume integralOur next proof is due to T.
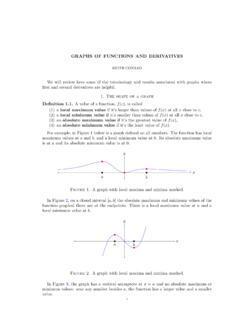
5 P. Jameson [5] and it was rediscovered by A. L. Delgado [3]. Revolvethe curvez=e 12x2in thexz-plane around thez-axis to produce the bell surface z=e 12(x2+y2).See below, where thez-axis is vertical and passes through the top point, thex-axis lies just underthe surface through the point 0 in front, and they-axis lies just under the surface through thepoint 0 on the left. We will compute the volumeVbelow the surface and above thexy-plane intwo we computeVbyhorizontal slices, which are discs:V= 10A(z) dzwhereA(z) is the areaof the disc formed by slicing the surface at heightz. Writing the radius of the disc at heightzasr(z),A(z) = r(z)2.
6 To computer(z), the surface cuts thexz-plane at a pair of points (x,e 12x2)where the height isz, soe 12x2=z. Thusx2= 2 lnz. Sincexis the distance of these points fromthez-axis,r(z)2=x2= 2 lnz, soA(z) = r(z)2= 2 lnz. ThereforeV= 10 2 lnzdz= 2 (zlnz z) 10= 2 ( 1 limz 0+zlnz).By L Hospital s rule, limz 0+zlnz= 0, soV= 2 . (A calculation ofVby shells is in [11].)Next we compute the volume byvertical slicesin planesx= constant. Vertical slices are scaledbell curves: look at the black contour lines in the picture. The equation of the bell curve along thetop of the vertical slice withx-coordinatexisz=e 12(x2+y2), whereyvaries andxis fixed.
7 Then4 KEITH CONRADV= A(x) dx, whereA(x) is the area of thex-slice:A(x) = e 12(x2+y2)dy=e 12x2 e 12y2dy=e A(x) dx= e 12x2 Idx=I e 12x2dx= the two formulas forV, we have 2 =I2, soI= 2 . proof : The -functionFor any integern 0, we haven! = 0tne tdt. Forx >0 we define (x) = 0txe tdtt,so (n) = (n 1)! whenn 1. Using integration by parts, (x+ 1) =x (x). One of the basicproperties of the -function [15, pp. 193 194] is( ) (x) (y) (x+y)= 10tx 1(1 t)y GAUSSIAN INTEGRAL5 Setx=y= 1/2: (12)2= 10dt t(1 t).Note (12)= 0 te tdtt= 0e t tdt= 0e x2x2xdx= 2 0e x2dx= 2J,so 4J2= 10dt/ t(1 t). With the substitutiont= sin2 ,4J2= /202 sin cos d sin cos = 2 2= ,soJ= /2.
8 Equivalently, (1/2) = . Any method that proves (1/2) = is also a methodthat calculates 0e proof : Asymptotic estimatesWe will showJ= /2 by a technique whose steps are based on [16, p. 371].Forx 0, power series expansions show 1 +x ex 1/(1 x). Reciprocating and replacingxwithx2, we get( )1 x2 e x2 11 + allx any positive integern, raise the terms in ( ) to thenth power and integrate from 0 to 1: 10(1 x2)ndx 10e nx2dx 10dx(1 +x2) the changes of variablesx= sin on the left,x=y/ nin the middle, andx= tan on theright,( ) /20(cos )2n+1d 1 n n0e y2dy /40(cos )2n 2d .SetIk= /20(cos )kd , soI0= /2,I1= 1, and ( ) implies( ) nI2n+1 n0e y2dy nI2n will show that ask ,kI2k /2.
9 Then nI2n+1= n 2n+ 1 2n+ 1I2n+1 1 2 2= 2and nI2n 2= n 2n 2 2n 2I2n 2 1 2 2= 2,so by ( ) n0e y2dy /2. ThusJ= CONRADTo showkI2k /2, first we compute several values ofIkexplicitly by a recursion. Usingintegration by parts,Ik= /20(cos )kd = /20(cos )k 1cos d = (k 1)(Ik 2 Ik),so( )Ik=k 1kIk ( ) and the initial valuesI0= /2 andI1= 1, the first few values ofIkare computed andlisted in Table /2112(1/2)( /2)32/34(3/8)( /2)58/156(15/48)( /2)748/105 Table Table 1 we see that( )I2nI2n+1=12n+ 1 2for 0 n 3, and this can be proved for allnby induction using ( ). Since 0 cos 1 for [0, /2], we haveIk Ik 1 Ik 2=kk 1 Ikby ( ), soIk 1 Ikask.
10 Therefore ( )impliesI22n 12n 2= (2n)I22n 2asn . Then(2n+ 1)I22n+1 (2n)I22n 2asn , sokI2k /2 ask . This completes our proof thatJ= proof is closely related to the fifth proof using the -function. Indeed, by ( ) (k+12) (12) (k+12+12)= 10t(k+1)/2+1(1 t)1/2 1dt,and with the change of variablest= (cos )2for 0 /2, the INTEGRAL on the right is equal to2 /20(cos )kd = 2Ik, so ( ) is the same asI2nI2n+1= (2n+12) (12)2 (2n+22) (2n+22) (12)2 (2n+32)= (2n+12) (12)24 (2n+12+ 1)= (2n+12) (12)242n+12 (2n+12)= (12)22(2n+ 1).THE GAUSSIAN INTEGRAL7By ( ), = (1/2)2. We saw in the fifth proof that (1/2) = if and only ifJ= proof : Stirling s FormulaBesides the INTEGRAL formula e 12x2dx= 2 that we have been discussing, another placein mathematics where 2 appears is in Stirling s formula:n!