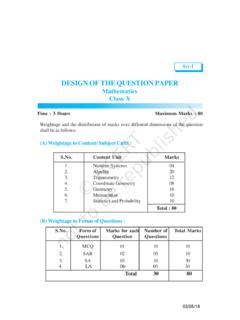
Transcription of APPLICATION OF INTEGRALS
1 APPLICATION OF INTEGRALS 359 Fig should study Mathematics because it is only through Mathematics thatnature can be conceived in harmonious form. BIRKHOFF IntroductionIn geometry, we have learnt formulae to calculate areasof various geometrical figures including triangles,rectangles, trapezias and circles. Such formulae arefundamental in the applications of mathematics to manyreal life problems. The formulae of elementary geometryallow us to calculate areas of many simple , they are inadequate for calculating the areasenclosed by curves. For that we shall need some conceptsof Integral the previous chapter, we have studied to find thearea bounded by the curve y = f (x), the ordinates x = a,x = b and x-axis, while calculating definite integral as thelimit of a sum. Here, in this chapter, we shall study a specificapplication of INTEGRALS to find the area under simple curves, area between lines and arcs of circles, parabolas andellipses (standard forms only).
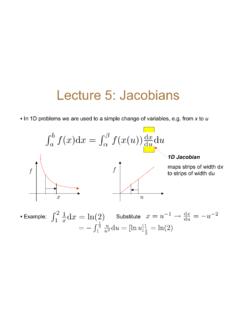
2 We shall also deal with findingthe area bounded by the above said under Simple CurvesIn the previous chapter, we have studieddefinite integral as the limit of a sum andhow to evaluate definite integral usingFundamental Theorem of Calculus. Now,we consider the easy and intuitive way offinding the area bounded by the curvey = f(x), x-axis and the ordinates x = a andx = b. From Fig , we can think of areaunder the curve as composed of largenumber of very thin vertical strips. Consideran arbitrary strip of height y and width dx,then dA ( area of the elementary strip)= ydx,where, y = f(x).Chapter8 APPLICATION OF Cauchy(1789-1857)360 MATHEMATICSFig area is called the elementary area which is located at an arbitrary positionwithin the region which is specified by some value of x between a and b. We can thinkof the total area A of the region between x-axis, ordinates x = a, x = b and the curvey = f (x) as the result of adding up the elementary areas of thin strips across the regionPQRSP.
3 Symbolically, we expressA = A( )bbbaaadydxf x dx== The area A of the region bounded bythe curve x = g (y), y-axis and the lines y = c,y = d is given byA = ( )ddccxdyg y dy= Here, we consider horizontal strips as shown inthe Fig If the position of the curve under consideration is below the x-axis, then sincef(x) < 0 from x = a to x = b, as shown in Fig , the area bounded by the curve, x-axisand the ordinates x = a, x = b come out to be negative. But, it is only the numericalvalue of the area which is taken into consideration. Thus, if the area is negative, wetake its absolute value, , ( )baf x dx .Fig , it may happen that some portion of the curve is above x-axis and some isbelow the x-axis as shown in the Fig Here, A1 < 0 and A2 > 0. Therefore, the areaA bounded by the curve y = f (x), x-axis and the ordinates x = a and x = b is givenby A = |A1| + OF INTEGRALS 361 Example 1 Find the area enclosed by the circle x2 + y2 = From Fig , the whole area enclosedby the given circle= 4 ( area of the region AOBA bounded bythe curve, x-axis and the ordinates x = 0 andx = a) [as the circle is symmetrical about bothx-axis and y-axis]= 04aydx (taking vertical strips)= 2204aax dx Since x2 + y2 = a2 gives y = 22ax As the region AOBA lies in the first quadrant, y is taken as positive.
4 Integrating, we getthe whole area enclosed by the given circle= 222 104sin22axaxaxa + = 2140sin 1022aa + = 22422aa = Fig , considering horizontal strips as shown in Fig , the whole area of theregion enclosed by circle= 04axdy = 2204aay dy (Why?)= 222104sin22aayyaya + = 2140sin 1022aa + = 2242 2aa = Example 2 Find the area enclosed by the ellipse 22221xyab+=Solution From Fig , the area of the region ABA B A bounded by the ellipse= in4,0, area of the region AOBAthe f irst quadrant boundedby the curve x axis and the ordinates xxa == (as the ellipse is symmetrical about both x-axis and y-axis)= 04(taking vert ical strips)aydx Now 2222xyab+ = 1 gives 22byaxa= , but as the region AOBA lies in the firstquadrant, y is taken as positive. So, the required area is= 2204abax dxa = 222 104sin22ab xaxaxaa + (Why?)= 2140sin 1022baaa + = 242 2b aaba = Fig OF INTEGRALS 363 Alternatively, considering horizontal strips asshown in the Fig , the area of the ellipse is= 04 bxdy = 2204 baby dyb (Why?)
5 = 222 104si n22ba ybybybb + = 2 140sin 1022abbb + = 242 2a babb = The area of the region bounded by a curve and a lineIn this subsection, we will find the area of the region bounded by a line and a circle,a line and a parabola, a line and an ellipse. Equations of above mentioned curves will bein their standard forms only as the cases in other forms go beyond the scope of 3 Find the area of the region boundedby the curve y = x2 and the line y = Since the given curve represented bythe equation y = x2 is a parabola symmetricalabout y-axis only, therefore, from Fig , therequired area of the region AOBA is given by402xdy = area of the region BONB bounded by curve,axis2and the lines0 and = 4yyy = = 402y dy = 4320223y 432833= =(Why?)Here, we have taken horizontal strips as indicated in the Fig , we may consider the verticalstrips like PQ as shown in the Fig toobtain the area of the region AOBA. To thisend, we solve the equations x2 = y and y = 4which gives x = 2 and x = , the region AOBA may be stated asthe region bounded by the curve y = x2, y = 4and the ordinates x = 2 and x = , the area of the region AOBA= 22ydx [y = (y-coordinate of Q) (y-coordinate of P) = 4 x2]= ()22024x dx (Why?)
6 =2302 43xx 82 4 23 = 323=Remark From the above examples, it is inferred that we can consider either verticalstrips or horizontal strips for calculating the area of the region. Henceforth, we shallconsider either of these two, most preferably vertical 4 Find the area of the region in the first quadrant enclosed by the x-axis,the line y = x, and the circle x2 + y2 = The given equations arey = (1)andx2 + y2 = (2)Solving (1) and (2), we find that the lineand the circle meet at B(4, 4) in the firstquadrant (Fig ). Draw perpendicularBM to the , the required area = area ofthe region OBMO + area of the , the area of the region OBMO= 4400ydxxdx= .. (3)= 42012x = 8 Fig 'BM(4 4),XX'(4 2 0), APPLICATION OF INTEGRALS 365OF (o)ae,BYY B'SRXX xae=Again, the area of the region BMAB= 4 24ydx = 4 22432x dx = 4 22 14113232 sin224 2xxx + = 1 1114114 2032sin 132 1632sin22222 + + = 8 (8 + 4 ) = 4 (4)Adding (3) and (4), we get, the required area = 4.
7 Example 5 Find the area bounded by the ellipse 22221xyab+= and the ordinates x = 0and x = ae, where, b2 = a2 (1 e2) and e < The required area (Fig ) of the region BOB RFSB is enclosed by theellipse and the lines x = 0 and x = that the area of the region BOB RFSB= 02aeydx = 2202aebax dxa = 222 102sin22aeb xaxaxaa + = 22 22 12sin2bae aa eaea + = 2 11sinab eee + EXERCISE the area of the region bounded by the curve y2 = x and the lines x = 1,x = 4 and the x-axis in the first the area of the region bounded by y2 = 9x, x = 2, x = 4 and the x-axis in thefirst the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis in thefirst the area of the region bounded by the ellipse 221169xy+=. the area of the region bounded by the ellipse 22149xy+=. the area of the region in the first quadrant enclosed by x-axis, line x =3yand the circle x2 + y2 = the area of the smaller part of the circle x2 + y2 = a2 cut off by the line 2ax=.
8 area between x = y2 and x = 4 is divided into two equal parts by the linex = a, find the value of the area of the region bounded by the parabola y = x2 and y = the area bounded by the curve x2 = 4y and the line x = 4y the area of the region bounded by the curve y2 = 4x and the line x = the correct answer in the following Exercises 12 and lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the linesx = 0 and x = 2 is(A) (B)2 (C)3 (D)4 of the region bounded by the curve y2 = 4x, y-axis and the line y = 3 is(A)2(B)94(C)93(D) area between Two CurvesIntuitively, true in the sense of Leibnitz, integration is the act of calculating the area bycutting the region into a large number of small strips of elementary area and thenadding up these elementary areas. Suppose we are given two curves represented byy = f (x), y = g (x), where f(x) g(x) in [a, b] as shown in Fig Here the points ofintersection of these two curves are given by x = a and x = b obtained by takingcommon values of y from the given equation of two setting up a formula for the integral, it is convenient to take elementary area inthe form of vertical strips.
9 As indicated in the Fig , elementary strip has heightAPPLICATION OF INTEGRALS 367yf x= ( )XYyg x= ( )xa=xc=yg x= ( )yf x= ( )xb=ABRCDQOPX Y f(x) g(x) and width dx so that the elementary areaFig = [f(x) g(x)] dx, and the total area A can be taken asA = [ ( )( )]baf xg x dx Alternatively,A =[ area bounded by y = f (x), x-axis and the lines x = a, x = b] [ area bounded by y = g (x), x-axis and the lines x = a, x = b]=( )( )bbaaf x dxg x dx =[]( )( ),baf xg x dx where f (x) g (x) in [a, b]If f (x) g (x) in [a, c] and f (x) g (x) in [c, b], where a < c < b as shown in theFig , then the area of the regions bounded by curves can be written asTotal area = area of the region ACBDA + area of the region BPRQB =[][]( )( )( )( )cbacf xg x dxg xf x dx + 368 MATHEMATICSYOP (4, 4)C (4, 0)Y X XQ (8, 0)Fig 6 Find the area of the region bounded by the two parabolas y = x2 and y2 = The point of intersection of these twoparabolas are O (0, 0) and A (1, 1) as shown inthe Fig , we can set y2 = x or y =x= f(x) and y = x2= g(x), where, f (x) g (x) in [0, 1].
10 Therefore, the required area of the shaded region= []10( )( )f xg x dx = 120x xdx 13320233xx = = 211333 =Example 7 Find the area lying above x-axis and included between the circlex2 + y2 = 8x and inside of the parabola y2 = The given equation of the circle x2 + y2 = 8x can be expressed as(x 4)2 + y2 = 16. Thus, the centre of thecircle is (4, 0) and radius is 4. Its intersectionwith the parabola y2 = 4x givesx2 + 4x =8xorx2 4x =0orx (x 4) =0orx = 0, x =4 Thus, the points of intersection of thesetwo curves are O(0,0) and P(4,4) above the Fig , the required area ofthe region OPQCO included between thesetwo curves above x-axis is= ( area of the region OCPO) + ( area of the region PCQP)= 4804ydxydx+ = 48220424(4)x dxxdx+ (Why?)Fig OF INTEGRALS 369= 43422200224, where,43xt dtxt + = (Why?)= 4222 1032144sin3224ttt + + = 2 1324104sin 1322 + + 32320 84323 =++ =+ = 4(8 3 )3+ Example 8 In Fig , AOBA is the part of the ellipse 9x2 + y2 = 36 in the firstquadrant such that OA = 2 and OB = 6.