Limits and Continuity for Multivariate Functions

1 Defining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesLimits and Continuity for Multivariate FunctionsA. HavensDepartment of MathematicsUniversity of Massachusetts, AmherstFebruary 25, 2019A. HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesOutline1 Defining Limits of Two Variable functions2 Case Studies in Two DimensionsAn Easy LimitFailure Along Different LinesLines Are Not EnoughAn Epsilon-Delta Game3 ContinuityDefining ContinuitySome Continuous Functions4 Three or more VariablesLimits and Continuity in Many VariablesDiscontinuities in Three DimensionsA. HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesDefinition of a Limit in two VariablesDefinitionGiven a function of two variablesf:D R,D R2such thatDcontains points arbitrarily close to a point (a,b), we say that thelimit off(x,y) as (x,y) approaches (a,b) exists and has valueLifand only if for every real number >0 there exists a real number >0 such that|f(x,y) L|< whenever0< (x a)2+ (y b)2<.

2 We then writelim(x,y) (a,b)f(x,y) = HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesInterpretationThus, to say thatLis the limit off(x,y) as (x,y) approaches(a,b) we require that for any given positive error >0, wecan find a bound >0 on the distance of an input (x,y)from (a,b) which ensures that the output falls within the errortolerance aroundL(that is,f(x,y) is no more than awayfromL).Another way to understand this is that for any given >0defining anopen metric neighborhood(L ,L+ ) ofLonthe number lineR, we can ensure there is a well defined ( )such that the image of any (possiblypunctured)open diskofradiusr< centered at (a,b) is contained in the HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesLimits along pathsRecall, for Functions of a single variable, one has notions ofleft andright one-sided Limits :limx a f(x)andlimx a+f(x).

3 But inR2there s not merely left and right to worry about; one canapproach the point (a,b) along myriad differentpaths! The wholelimit lim(x,y) (a,b)f(x,y) =Lif and only if the Limits along allpaths agree and HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesDefining Limits along pathsTo write a limit along a path, we can parameterize the path assome vector valued functionr(t) withr(1) = a,b , and then wecan writelimt 1 f(r(t)) =Lif for any >0, there is a >0 such that|f(r(t)) L|< whenever 1 <t<1. Similarly we may define a right limitalongr(t), limt 1+f(r(t)) ifr(t) exists and describes a continuouspath fort>1. The two sided limit along the path is then definedin the natural way:limt 1f(r(t)) =L >0 >0 :|f(r(t)) L|< whenever 0<|1 t|< .A. HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesAn Easy LimitA Classic RevistedExampleLetf(x,y) =sin(x2+y2)x2+y2.

4 Then findlim(x,y) (0,0)f(x,y).Solution:We can compute the limit as follows. Letr2=x2+y2. Thenalong any pathr(t) = x(t),y(t) such that ast 1,r(t) 0,we have thatr2= r 2 0. It follows thatlim(x,y) (0,0)f(x,y) = limr2 0sinr2r2= limu 0sinuu= HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesAn Easy LimitA Surface of RevolutionThe previous example has a geometric solution as well: the graphforz=f(x,y) = sin(r2)/r2is a surface of revolution. What is thecurve revolved, and what is the axis?Figure: The graph ofz= sin(r2) HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesFailure Along Different LinesA Non-Existent LimitExampleShow thatlim(x,y) (0,0)f(x,y) does not exist forf(x,y) =x2 y2x2+ : We will show that the Limits along thexandyaxes aredifferent, thus showing that the limit cannot HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesFailure Along Different LinesThe Axial LimitsExampleAlong thex-axis,y= 0, and sof(x,y) =f(x,0) =x2 0x2+ 0= 1,whencelimx 0f(x,0) = they-axis,x= 0 andf(x,y) =f(0,y) =0 y20 +y2= 1,whencelimy 0f(0,y) = limx 0f(x,0)6= limy 0f(0,y), the limitlim(x,y) (0,0)f(x,y) doesnot HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesFailure Along Different LinesSeeing the CreaseFigure: The graph ofz= (x2 y2)/(x2+y2)A.

5 HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesLines Are Not EnoughA Curious WrinkleExampleDoes the limit off(x,y) =xy2x2+y4as (x,y) (0,0) exist, and ifyes, what is it?Solution: A simple reapplication of the method of the previousexample is not sufficient. Indeed, you can check thatlimx 0f(x,0) = 0 = limy 0f(0,y),and in fact, we can show that for any line of approach through(0,0), the limit is HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesLines Are Not EnoughAll the (defined) slopesExampleIndeed: letmbe any real number and consider the liney=mx,which passes through (0,0) asx 0. Thenlimx 0f(x,mx) = limx 0x(mx)2x2+ (mx)4= limx 0m2x3x2+m4x4= limx 0m2x1 +m4x2= 0,regardless of the value ofm. (In the case of a line of undefinedslope, we simply have they-axis, which shares this limit)So is the limit 0?

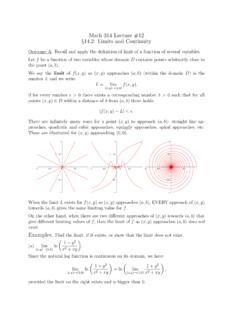
6 A. HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesLines Are Not EnoughPrecarious ParabolaeFigure: The graph ofz= (xy2)/(x2+y4)A. HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesLines Are Not EnoughA new pathExampleIf we instead approach (0,0) along the parabolax=y2, we findthatlimy 0f(y2,y) = limy 0y4y4+y4=126= the limit does not exist!Key moral: Given the complexity of surface discontinuities(creases, wrinkles, precipitous slopes, etc), one cannot trust thatthe limit exists just from testing some small family of a limit does exist, proving it via curves is impractical, andone must resort to the definition (working with s and s.)A. HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesAn Epsilon-Delta GameUsing the Definition to Prove a LimitExampleConsider the functionf(x,y) =3xy2x2+ intuition for this one might be that the limit is zero as(x,y) (0,0).

7 After all, the numerator is cubic, and thedenominator quadratic, so we can guess who should win in a testing out lines, parabolas, and even some cubicsapproaching (0,0), one gets that the Limits along these curves allgo to 0. How can we show that the limit is indeed zero?A. HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesAn Epsilon-Delta GameAll Paths Lead : The graph ofz= 3xy2/(x2+y2).A. HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesAn Epsilon-Delta GameTo Acquire a Delta, Fix and EpsilonExampleSuppose we are given an >0, and we know that|f(x,y) 0|< for some (x,y).We wish to work backwards to figure out how close to (0,0) thepoint (x,y) must be to ensure that this inequality is resulting bound on distance, , will depend on .A. HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesAn Epsilon-Delta GameInequalities and AlgebraFrom the assumed bound|f(x,y) 0|< = 3xy2x2+y2 = 3|x|y2x2+y2< and the following inequalitiesx2 x2+y2and 0 y2/(x2+y2) 1we have that3|x|y2x2+y2 3|x|= 3 x2 3 x2+ see the distance between (x,y) and (0,0) appearing on the farright in the HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesAn Epsilon-Delta GameEpsilong Proofs: When s the punchline?

8 Since 3 times this distance is an upper bound for|f(x,y) 0|, wesimply choose to ensure 3 x2+y2< . Thus, we may take = provided = /3, we have that whenever 0< x2+y2< ,the inequality3 x2+y2< holds, whence|f(x,y) 0|= 3|x|y2x2+y2 3 x2+y2< ,which proves thatlim(x,y) (0,0)3xy2x2+y2= HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesDefining ContinuityLocal ContinuityDefinitionA function of two variablesf:D Ris continuous at a point(x0,y0) Dif and only iff(x0,y0) =lim(x,y) (x0,y0)f(x,y), , the function is defined at (x0,y0), its limit exists as (x,y)approaches (x0,y0), and the function s value there is equal to thevalue of the HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesDefining ContinuityContinuity Throughout the DomainA function is said to becontinuous throughout its domain, orsimply is calledcontinuous, if it is continuous at every point(x0,y0) of its functionf:D Ris continuous throughoutDif and only ifthe pre-image of any open interval (a,b) ={t:a<t<b} Risan open subset of the domain.

9 In this context, an open setE R2is one for which around every pointp Ethere is some open diskcentered atpcontained fully inE, and an open subset ofDis aset which can be made as the intersection ofDwith an open set inR2. For technical reasons, the empty set and the whole of thedomainDare considered open subsets of the HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesSome Continuous FunctionsWell Behaved FriendsPolynomials in two variables are continuous on all ofR2. Recall apolynomial in two variables is an expression of the formp(x,y) =m i=0n j= Functions are also continuous on their domains. Rationalfunctions of two variables are just quotients of two variablepolynomialsR(x,y) =p(x,y)/q(x,y). Observe thatDom p(x,y)/q(x,y) ={(x,y) R2:q(x,y)6= 0}.A. HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesSome Continuous FunctionsA removable discontinuityIf a functionfhas a discontinuity at a point (a,b), butlim(x,y) (a,b)f(x,y) exists and equalsL, then the function f(x,y) =lim(u,v) (x,y)f(u,v) ={f(x,y)if (x,y) DLif (x,y) = (a,b)is continuous at (a,b).}

10 , the functionR(x,y) =lim(u,v) (x,y)3uv2u2+v2= 3xy2x2+y2if (x,y)6= (0,0)0if (x,y) = (0,0)is continuous at (0,0), and as it is elsewhere rational with only(0,0) as a zero of its denominator,R(x,y) is in fact HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesSome Continuous FunctionsExampleWhere isf(x,y) = arctan(yx)continuous?Solution: Since arctan is continuous throughout its domain, thisfunction is continuous provided the argumenty/xis this argument is a rational function, it is well definedeverywhere inR2except for points (x,y) such that thedenominator is , we conclude that arctan yx is continuous onR2 {x= 0}, , the whole plane except HavensLimits and Continuity for Multivariate FunctionsDefining Limits of Two Variable functionsCase Studies in Two DimensionsContinuityThree or more VariablesSome Continuous FunctionsAngular SurfaceFigure: The graph ofz= arctan(y/x).A.