Applications of the Fourier Series

1 Applications of the Fourier SeriesMatt HollingsworthAbstractThe Fourier Series , the founding principle behind the field of Fourier Analysis, is an infiniteexpansion of a function in terms of sines and cosines. In physics and engineering, expanding functionsin terms of sines and cosines is useful because it allows one to more easily manipulate functions thatare, for example, discontinuous or simply difficult to represent analytically. In particular, the fieldsof electronics, quantum mechanics, and electrodynamics all make heavy use of the Fourier , other methods based on the Fourier Series , such as the FFT (Fast Fourier transform a form of a Discrete Fourier transform [DFT]), are particularly useful for the fields of Digital SignalProcessing (DSP) and Spectral numbers:I.

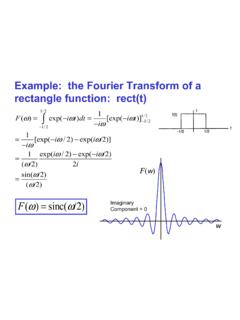
2 INTRODUCTIONThe Fourier Series , the founding principle behind thefield of Fourier Analysis, is an infinite expansion of a func-tion in terms of sines and cosines or imaginary exponen-tials. The Series is defined in its imaginary exponentialform as follows:f(t) = n= Aneinx(1)where theAn s are given by the expressionAn=12 f(x)e inxdx(2)Thus, the Fourier Series is an infinite superpositionof imaginary exponentials with frequency terms that in-crease as n increases. Since sines and cosines (and in turn,imaginary exponentials) form an orthogonal set1, this se-ries converges for any moderately well-behaved functionf(x). Examples of the Fourier Series for different wave-forms are given in figure THE FAST Fourier TRANSFORMThe Fourier Series is only capable of analyzing the fre-quency components of certain, discreet frequencies (in-tegers) of a given function.

3 In order to study the casewhere the frequency components of the sine and cosineterms are continuous, the concept of the Fourier Trans-form must be introduced. The imaginary exponentialform of the Fourier transform is defined as follows:H( ) = h(t)ei tdt(3)h(t) =12 H( )e i td (4)FIG. 1: Fourier Series ExamplesHere, theH(w) fulfills the role of theAn s in equations(1) and (2); it gives an indicator of how much a par-ticular frequency oscillation contributes to the functionf(t).Assume that we have a equidistant, finite data sethk=h(tk),tk=k , and we are only interested inNequidistant, discreet frequencies in the range cto thus wish to examine the frequencieswn=2 nN , forN= N2.

4 ,N2, where we let be the same whichdefines ourtk s. We may provide an approximation tothe Fourier transform in this range by a Riemann sumas follows3:H( n) = h(t)ei tdt N 1 k=0hkei ntk Using our definition oftk, this expression reduces toH( ) N 1 k=0hkeik2 nN(5)2 This equation is called the Discreet Fourier transform (DFT) of the functionh(t). If we denoteHnasHn=N 1 k=0hkeik2 nN(6)the Fourier transform ,H( ), may then be approxi-mated using the expressionH( ) Hn(7)Comparing equation (6) with the Fourier Series givenin equation (1), it is clear that this is a form of the FourierSeries with non-integer frequency , the most common and efficient method ofnumerically calculating the DFT is by using a class of al-gorithms called Fast Fourier Transforms (FFTs).

5 Thefirst known discovery of the FFT was by Gauss in 1805;however, the first modern rediscovery of the FFT wasdone in 1942 by Danielson and Lanczos4. They wereable to show one may divide any DFT into a sum of twoDFT s which each correspond toN2 1 proof of Danielson and Lanczos s assertion is thefollowing4:First, defineWas the complex numberW=e2 i/N(8)Equation (6) may then be writtenHn=N 1 k=0 Wnkhk(9)Any DFT may then be written as follows:Hn=N 1 k=0e2 ink/Nhn=N/2 1 k=0e2 i(2k)n/Nh2k+N/2 1 k=0e2 i(2k+1)n/Nh2k+1=N/2 1 k=0e2 i(2k)n/(N/2)h2k+WkN/2 1 k=0e2 i(2k)n/(N/2)h2k+1=Hen+WkHOnHere,Hendenot es the even terms of the sum (the onescorresponding to the index 2k) andHOndenotes the oddterms (the ones corresponding to the index 2k+ 1).

6 The most useful part of this formula is that it can beused recursively, since each of theseHenandHOntermsmay be independently expanded using the same algo-rithm, each time reducing the number of calculations bya factor of 2. In fact, this class of FFT algorithm shrinksthe compution time fromO(N2) operations to the muchmore manageableO(Nlog2N) operations. There aremany different FFT algorithms; the one presented here issimply the most common one, known as a Cooley-TukeyFFT algorithm. There are other algorithms which candecrease computation time by 20 or 30 percent (so-calledbase-4 FFTsorbase-8 FFTs)4. Most importantly, bothclasses of FFT algorithms are fast enough to embed intomodern digital oscilloscopes and other such electronicequipment.

7 Thus, FFTs have many modern Applications ,such as Spectrum Analyzers, Digital Signal Processors(DSPs), and the numerical computation arbitrary-sizemultiplication THE SPECTRUM ANALYZERAn important instrument to any experimentalist is thespectrum analyzer. This instrument reads a signal (usu-ally a voltage) and provides the operator with the Fouriercoefficients which correspond to each of the sine and co-sine terms of the Fourier expansion of the signal. Sup-pose an instrument takes a time-domain signal, such asthe amplitude of the output voltage of an us call this signal V(t). Then the DFT of V(t) isHn=N 1 k=0vkeik2 nN(10)We see that this equation is of the same form ofequation (6), which means that the previously describedmethods of the FFT apply to the function.

8 Thus, anydigital oscilloscope that is sufficiently fast and equippedwith a FFT algorithm is capable of providing the userwith the frequency components of the source which are equipped with the ability toFFT their inputs are termed Digital Spectral Analyz-ers . Although they were once a separate piece of equip-ment for experimentalists, improvements in digital elec-tronics has made it practical to merge the role of oscil-loscopes with that of the Spectral Analyzer; it is quitecommon now that FFT algorithms come built into Analyzers have many uses in the laboratory,but one of the most common uses is for signal noise stud-ies.

9 As shown above, the FFT of the signal gives theamplitudes of the various oscillatory components of theinput. After normalization, this allows for the experi-mentalist to determine what frequencies dominate theirsignal. For example, if you have a DC signal, you wouldexpect the FFT to show only very low frequency oscil-lations ( , the largest amplitudes should correspond tof 0). However, if you see a sharp peak of amplitudesaround 60 Hz, you would know that something is feed-ing noise into your signal with a frequency of 60 Hz (forexample, an AC leakage from your power source).3IV. DIGITAL SIGNAL PROCESSINGWe have already seen how the Fourier Series allowsexperimentalists to identify sources of noise.

10 It may alsobe used to eliminate sources of noise by introducing theidea of theInverse Fast Fourier transform (IFFT).In general, the goal of an Inverse Fourier transform is totake theAn(the ones that appear in eq (5) and use themto reconstruct the original function,f(t).Analytically, this is done by multiplying eachAnbye2 iknNthen taking the sum over all n. However, thisis an inefficient algorithm to use when the calculationmust be done numerically. Just as there is a fast numer-ical algorithm for approximating the Fourier coefficients(the FFT), there is another efficient algorithm, called theIFFT, which is capable of calculating the Inverse FourierTransform much faster than the brute-force 1988, it was shown by Duhamel, Piron, and Etcheto7that the IFFT is simplyF 1(x) =F(ix ) (11)In other words, you can calculate the IFFT directlyfrom the FFT; you simply flip the real and imaginaryparts of the coefficients calculated by the original , the IFFT algorithms are essentially the same asthe FFT algorithms.)