ECUACIÓN GENERAL DE UNA ELIPSE

1 Unidad 4 ELIPSE , Circunferencia y sus ecuaciones cartesianas 4 - 28 ECUACI N GENERAL DE UNA ELIPSE Hasta aqu hemos presentado las ecuaciones de elipses en la forma que lla-mamos ordinaria, donde los cuadrados de los binomios se quedan indicados. Esta forma nos fue muy til para identificar con rapidez los valores de par -metros a y b, as como las coordenadas del centro (h, k). Ahora obtendremos la llamada forma GENERAL de la ecuaci n de la ELIPSE , desarrollando los cuadrados indicados en la forma ordinaria y reagrupando algu-nos t rminos. Para la ELIPSE horizontal con centro C(h, k) 1)()(2222 bkyahx Efectuando un proceso algebraico en el que eliminamos los denominadores, desarrollamos los binomios al cuadrado, agrupamos t rminos semejantes e igua-lamos a cero, obtenemos la ecuaci n: 022222222222222 bakahbkyahxbyaxb En la que podemos renombrar los coeficientes constantes y expresarla as : 022 FEyDxCyAx, que es la buscada ecuaci n GENERAL de una elip-se horizontal con centro C(h, k).

2 Para la ELIPSE vertical con centro C(h, k) 1)()(2222 akybhx. Siguiendo el mismo proceso algebraico que para la ELIPSE horizontal, llegamos a la ecuaci n: 022222222222222 bakbhakybhxaybxa En la que podemos renombrar los coeficientes constantes y expresarla as : 022 FEyDxCyAx, que es la ecuaci n GENERAL de una ELIPSE vertical con centro C(h, k). De lo anterior se puede concluir que la ecuaci n de una ELIPSE con centro en un punto cualquiera y ejes paralelos a los coordenados, siempre puede expresar-se en la forma GENERAL : 4 - 29 Unidad 4 ELIPSE , Circunferencia y sus ecuaciones cartesianas 022 FEyDxCyAx Donde los coeficientes A y C ser n diferentes de cero y del mismo signo.

3 Sugerencias para quien imparte el curso Recomendamos preguntar a los alumnos c mo distinguir, si la ELIPSE es horizontal o vertical teniendo solamente la ecuaci n en su forma GENERAL . Dependiendo de las combinaciones de valores con los otros coeficientes, la ecuaci n GENERAL podr a representar s lo un punto o ning n lugar geom trico real. Inversamente: una ecuaci n de segundo grado que carece del t rmino xy, en la que los coeficientes de los t rminos en x2 y y2 tienen el mismo signo, representa una ELIPSE con ejes paralelos a los ejes coordenados, un punto o ning n lugar geom trico real.

4 Expresar en forma GENERAL cada una de las siguientes ecuacio-nes dadas en forma ordinaria. 1. 149)2(36)5(22 yx 2. 17)4(16)1(22 yx 3. 164)3(2522 yx Intentemos el problema inverso. C mo expresar en forma ordinaria la ecuaci n de una ELIPSE dada en forma GENERAL ? Ejercicio 1 Unidad 4 ELIPSE , Circunferencia y sus ecuaciones cartesianas 4 - 30 Dada la ecuaci n 22494054145 0xyxy , Indicar de qu curva se trata, obtener sus elementos y graficarla Expres mosla en forma ordinaria, de manera que podamos obtener m s in-formaci n sobre esta posible ELIPSE (centro, focos, v rtices, etc.)

5 , para lograrlo rea-liza el procedimiento siguiente: 1. Dejar en el primer miembro los t rminos que tienen x y los que tienen y, agrup ndolos seg n la variable. 22440954145xxyy 2. Factorizar el 4 para los t rminos en x y el 9 para los de y 224(10 ) 9(6 )145xxyx 3. Completar trinomios cuadrados perfectos dentro de cada par ntesis, su-mando lo que sea necesario a ambos miembros de la igualdad 224(1025) 9(69)145 100 81xxyx 4. Factorizar los trinomios cuadrados perfectos, como binomios al cuadrado y reducir t rminos semejantes 224(5)9(3)36xy 5.

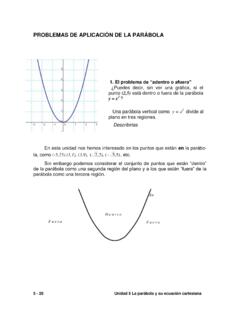
6 Dividir la ecuaci n entre 36, obteniendo 2253194xy As , llegamos a una ecuaci n con la que estamos m s familiarizados. De qu curva se trata, es horizontal o vertical? Dar las coordenadas del centro, el valor de cada una de las constantes a, b y c, las coordenadas de los fo-cos, de los v rtices, la excentricidad, la longitud de los ejes mayor, menor y del lado recto. La ELIPSE es horizontal. Ejemplo 5 4 - 31 Unidad 4 ELIPSE , Circunferencia y sus ecuaciones cartesianas Las coordenadas del centro son 5, 3C . El valor de cada una de las constantes es 3,2,9 45abc Las coordenadas de los focos son 55, 3 55, 3Fy F Las coordenadas de los v rtices son 8, 3 2, 3Vy V La excentricidad es 53e La longitud del lado recto es 83 Y su gr fica es: Hagamos las transformaciones algebraicas necesarias para llevar esta ecua-ci n GENERAL a la forma ordinaria.

7 1. x2 12x + 8y2 16y = 36 2. (x2 - 12x) + 8 (y2 2y) = 36 Ejemplo 6 Dada la ecuaci n x2 + 8y2 12x 16y 36 = 0, encontrar todas las caracter sticas de la curva que representa. Unidad 4 ELIPSE , Circunferencia y sus ecuaciones cartesianas 4 - 32 3. Completando los trinomios cuadrados perfectos. (x2 - 12x + 36) + 8 (y2 2y + 1) = 36 + (36) + 8 (1) 4. Factorizando: ( x - 6)2 + 8 (y - 1)2 = 80 5. Dividiendo entre 80: 8080801880622 yx Esta ecuaci n puede escribirse en la forma con la que estamos m s familia-rizados: 110180622 yx a) De qu curva se trata?

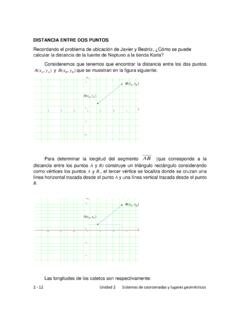
8 B) Es horizontal o vertical? Es horizontal c) Las coordenadas del centro son C 6,1C d) El valor de cada una de las constantes es: 80,10,ab 80 1070c e) Las coordenadas de los focos son 670,1 670,1Fy F f) Las coordenadas de los v rtices son 680,1 680,1Vy V . g) La excentricidad es 7080e . h) La longitud de los ejes es: eje mayor =2 80 , eje menor =2 10 y i) La longitud del lado recto es 2080 Y su gr fica se muestra enseguida: 4 - 33 Unidad 4 ELIPSE , Circunferencia y sus ecuaciones cartesianas Expres mosla en forma ordinaria, de manera que podamos obtener m s in-formaci n sobre esta ELIPSE (centro, focos, v rtices, etc.

9 1. Dejamos en el primer miembro los t rminos que tienen x y los que tienen y, agru-p ndolos seg n la variable: 49x2 196x + 25y2 - 300y = 129. 2. Factorizamos el 49 para los t rminos en x y el 25 para los de y: 224942512129xxyy . 3. Completamos trinomios cuadrados perfectos dentro de cada par ntesis, sumando lo que sea necesario a ambos miembros de la igualdad: 224944251236129 49(4) 25(36)xxyy 4. Factorizamos los trinomios cuadrados perfectos, como binomios al cua-drado y reduciendo t rminos semejantes: 224922561225xy 5. Dividimos entre 1225 toda la ecuaci n: 224922561225122512251225xy 6.

10 Reduciendo las fracciones: 222612549xy Ejemplo 7 Dada la ecuaci n de segundo grado, en dos variables y sin t rmino en xy: ,realizar lo siguien-te: a)Identificar el tipo y posici n de la curva. b)Obtener las coordenadas del centro, de los fo-cos y de los v rtices. c)Escribir las longitudes de los ejes y del lado recto. d)Calcular la excentricidad de la curva. Unidad 4 ELIPSE , Circunferencia y sus ecuaciones cartesianas 4 - 34 Observamos que se trata de una ELIPSE y es vertical Las coordenadas del centro son: 2, 6C El valor de cada uno de los par metros 7,5,49 2524abc Las coordenadas de los focos son 2, 624 2, 624Fy F Los v rtices son los puntos 2,1 2, 13Vy V b) La excentricidad es 247e.