Distributions related to the normal distribution - Website

1 Distributions related to the normal distribution Three important Distributions : Chi-square ( 2 ) distribution . t distribution . F distribution . Before we discuss the 2 , t, and F Distributions here are few important things about the gamma ( ) distribution . The gamma distribution is useful in modeling skewed Distributions for variables that are not negative. A random variable X is said to have a gamma distribution with parameters , if its probability density function is given by x x 1 e . f (x) = , , > 0, x 0. ( ). E(X) = and 2 = 2 . A brief note on the gamma function: The quantity ( ) is known as the gamma function and it is equal to: Z . ( ) = x 1 e x dx.

2 0. Useful result: 1 . ( ) = . 2. If we set = 1 and = 1 we get f (x) = e x . We see that the exponential distribution is a special case of the gamma distribution . 1. The gamma density for = 1, 2, 3, 4 and = 1. Gamma distribution density ( = 1,, = 1). ( = 2,, = 1). f(x). ( = 3,, = 1). ( = 4,, = 1). 0 2 4 6 8. x Moment generating function of the X ( , ) random variable: MX (t) = (1 t) . Proof: x Z 1 Z . tx x e 1 1 t tX 1 x( ). MX (t) = Ee = e dx = x e dx 0 ( ) ( ) 0. Let y = x( 1 t . ) x= . 1 t y, and dx = . 1 t dy. Substitute these in the expression above: Z ! 1. 1 . MX (t) = y 1 e y dy ( ) 0 1 t 1 t ! 1. 1 Z 1 y MX (t) = y e dy MX (t) = (1 t) . ( ) 1 t 1 t 0.

3 2. Theorem: Let Z N (0, 1). Then, if X = Z 2 , we say that X follows the chi-square distribution with 1. degree of freedom. We write, X 21 . Proof: 1 2. Find the distribution of X = Z 2 , where f (z) = 12 e 2 z . Begin with the cdf of X: . FX (x) = P (X x) = P (Z 2 x) = P ( x Z x) .. FX (x) = FZ ( x) FZ ( x). Therefore: 1 1 1 1 1 1 1 1 1 1 x fX (x) = x 2 e 2 x + x 2 e 2 x = 1 x 2 e 2 , or 2 2 2 2 22 . 1 x x 2 e 2. fX (x) = 1 . 2 2 ( 12 ). This is the pdf of ( 21 , 2), and it is called the chi-square distribution with 1 degree of freedom. We write, X 21 . 1. The moment generating function of X 21 is MX (t) = (1 2t) 2 . Theorem: Let Z1 , Z2 , .. , Zn be independent random variables with Zi N (0, 1).

4 If Y = ni=1 zi2 then P. Y follows the chi-square distribution with n degrees of freedom. We write Y 2n . Proof: Find the moment generating function of Y . Since Z1 , Z2 , .. , Zn are independent, MY (t) = MZ12 (t) MZ22 (t) .. MZn2 (t). 1. Each Zi2 follows 21 and therefore it has mgf equal to (1 2t) 2 . Conclusion: n MY (t) = (1 2t) 2 . This is the mgf of ( n2 , 2), and it is called the chi-square distribution with n degrees of free- dom. Theorem: Let X1 , X2 , .. , Xn independent random variables with Xi N ( , ). It follows directly form the previous theorem that if n 2. xi . then Y 2n . X. Y =. i=1 . 3. We know that the mean of ( , ) is E(X) = and its variance var(X) = 2.

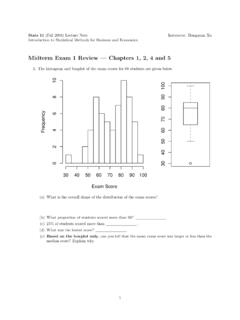
5 Therefore, if X 2n it follows that: E(X) = n, and var(x) = 2n. Theorem: Let X 2n and Y 2m . If X, Y are independent then X + Y 2n+m . Proof: Use moment generating functions. Shape of the chi-square distribution : In general it is skewed to the right but as the degrees of freedom increase it becomes N (n, 2n). Here is the graph: 23. f(x). 0 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 64 68 72 76 80 84 88 92 96. x 210. f(x). 0 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 64 68 72 76 80 84 88 92 96. x 230. f(x). 0 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 64 68 72 76 80 84 88 92 96. x 4. The 2 distribution - examples Example 1. If X 216 , find the following: a.

6 P (X < ). b. P (X > ). c. P ( < X < ). d. If P (X < b) = , find b. e. If P (X < c) = , find c. Example 2. If X 212 , find constants a and b such that P (a < X < b) = and P (X < a) = Example 3. If X 230 , find the following: a. P ( < X < ). b. Constants a and b such that P (a < X < b) = and P (X < a) = c. The mean and variance of X. Example 4. If the moment-generating function of X is MX (t) = (1 2t) 60 , find: a. E(X). b. V ar(X). c. P ( < X < ). 5. Theorem: Let X1 , X2 , .. , Xn independent random variables with Xi N ( , ). Define the sample variance as n 1 X (n 1)S 2. S2 = (xi x )2 . Then 2n 1 . n 1 i=1 2. Proof: Example: Let X1 , X2 , .. , X16 random variables from N (50, 10).

7 Find n ! 2. X. a. P < (Xi 50) < 2630 . i=1. n ! < 2500 . 2. X. b. P < (Xi X). i=1. 6. The 21 (1 degree of freedom) - simulation A random sample of size n = 100 is selected from the standard normal distribution N (0, 1). Here is the sample and its histogram. [1] [5] [9] [13] [17] [21] [25] [29] [33] [37] [41] [45] [49] [53] [57] [61] [65] [69] [73] [77] [81] [85] [89] [93] [97] Histogram of the random sample of n=100. Density 2 1 0 1 2. z 7. The squared values of the sample above and their histogram are shown below. [1] +00. [5] +00 +00 +00. [9] +00. [13] [17] +00 +00 [21] +00 [25] +00 +00. [29] [33] +00 [37] +00 +00. [41] +00 [45] +00 [49] [53] [57] +00 [61] +00 [65] +00 +00 [69] +00 +00 [73] [77] +00 +00 +00.

8 [81] [85] +00 +00 [89] +00 +00 +00. [93] +00 +00 [97] +00. Histogram of the squared values of random sample of n=100. Density 0 1 2 3 4. z2. 8. The t distribution Definition: Let Z N (0, 1) and U 2df . If Z, U are independent then the ratio Z. q U. follows the t (or Student's t) distribution with degrees of freedom equal to df . df We write X tdf . The probability density function of the t distribution with df = n degrees of freedom is ! n+1. ( n+1 ) x2 2. f (x) = 2 n 1 + , < x < . n ( 2 ) n n Let X tn . Then, E(X) = 0 and var(X) = n 2 . The t distribution is similar to the standard normal distribution N (0, 1), but it has heavier tails. However as n the t distribution converges to N (0, 1) (see graph below).

9 N(0,, 1). t15. t5. f(x). t1. x 9. Application: Let X1 , X2 , .. , Xn be independent and identically distributed random variables each one 2 . having N ( , ). We have seen earlier that (n 1)S. 2. 2n 1 . We also know that X .. N (0, 1). n We can apply the definition of the t distribution (see previous page) to get the following: . X .. n . X. = . s r (n 1)S 2. 2 n n 1.. X . Therefore s tn 1 . n . X . Compare it with . N (0, 1). n Example: Let X and SX 2. denote the sample mean and sample variance of an independent random sample of size 10 from a normal distribution with mean = 0 and variance 2 . Find c so that . X . P q < c = 2. 9SX. 10. The F distribution Definition: Let U 2n1 and V 2n2.

10 If U and V are independent the ratio U. n1. V follows the F distribution with numerator n1 and denominator n2 . n2. We write X Fn1 ,n2 . The probability density function of X Fn1 ,n2 is: n1 1 (n1 +n2 ). ( n1 +n2 ) n1 n1.. 2 n2 2. 1. f (x) = n1 2 n2 x 2 1+ x , 0 < x < . ( 2 ) ( 2 ) n2 n2. Mean and variance: Let X Fn1 ,n2 . Then, n2 2n22 (n1 + n2 2). E(X) = , and var(X) = . n2 2 n1 (n2 2)2 (n2 4). Shape: In general the F distribution is skewed to the right. The distribution of F10,3 is shown below: f(x). 0 1 2 3 4 5 6. x 11. Application: Let X1 , X2 , .. , Xn random variables from N ( X , X ). Let Y1 , Y2 , .. , Ym random variables from N ( Y , Y ). If X and Y are independent the ratio 2.